There exists a pile of matches and there are two players who move alternately. Each player divides a pile of matches into two unequal piles. If a player is unable so to divide then in the misere game he is the winner, but in the ordinary game he is the loser.
In the accompanying table below the situations are indicated for the various games.
Note for some games A can win in either game and this is indicated by a question mark ?
To generalise the game beyond that shown consider the case of 13
NORMAL MISERE
12 & 1 W & L L & W
11 & 2 ? & L ? & W
10 & 3 L & W W & L
9 & 4 W & L L & W
8 & 5 ? & ? ? & ?
7 & 6 L & W W & L
The resulting piles must be (W & W) or (L & L). Subject to their being an even number of ?
Best move is 11,2 or 8,5.
number of value move value move
matches ordinary misere
1 L - W -
2 L - W -
3 W 2,1 L -
4 L - W 3,1
5 ? 4,1 ? 3,2
6 W 4,2 L -
7 L - W 6,1
8 ? 7,1 ? 6,2
9 W 7,2 L -
10 L - W 9,1
11 ? 10,1 ? 9,2
12 W 10,2 L -
13 ? 8,5 ? 8,5
14 ? 10,4 ? 12,2
15 W 12,3 L -
16 ? 11,5 ? 11,5
17 ? 10,7 ? 15,2
18 W 15,3 L -
19 ? 11,8 ? 11,8
20 L - L -

The Normal Version
Therefore, in the normal version, if the player playing first is to win, there will be an odd number of moves in the game. For example, if there are 3 matches in the starting pile, the first player will split these into 2 and 1. The second player is unable to play. Therefore, after one move, the first player has won. It follows that for the first player to lose, there will be an even number of moves in the game. We can use this fact to build up a table. If we split a pile into two piles
which both result in either wins or losses for the first player, the game will consist of an odd number of moves.
the split + a win game + a win game the split + a lose game + a lose game
So, 1 and 2 are both lose games, so 3 goes to 1 and 2 which are both loses, meaning that 3 is a win. The table up to 20 then progresses as:
1 L
2 L
3 W (1,2)
4 L
5 W (1,4)
6 W (2,4)
7 L
8 W (1,7)
9 W (2,7)
10 L
11 W (1,10)
12 W (2,10)
13 W (5,8)
14 W (3,11)
15 W (6,9)
16 W (3,13)
17 W (7,10)
18 W (3,15)
19 W (3,16)
20 W (3,17)
Let us consider the case of 14.
Player A 11,3
Player B 9,5
This leaves two win piles, that is, an even number of moves in the game. Player B has won !
Why is this ? It is because we have not considered the possibility that a pile may be split in an alternative manner so as to guarantee a defeat. A defeat occurs when we split a pile into one win and one lose pile. For example, we split 5 into 1 and 4 in order to guarantee a win, but we may also split it into 2 and 3 in order to guarantee a loss.
This is useful because it means that piles such as 5,8 and 11 are decision points where the number of moves left in the game can be altered. ( Remember there is only one moves difference between a win and a loss. ) Therefore, in the 14 example, once player A had split 14 into 3 and 11, he has lost because player B could now split the 11 in the necessary way to guarantee victory. This discovery means that we now have to redraw our table showing these decision points.
1 L
2 L
3 W (1,2)
4 L
5 ? W (1,4) L (2,3)
6 W (2,4)
7 L
8 ? W (1,7) L (2,6)
9 W (2,7)
10 L
11 ? W (1,10) L (2,9)
12 W (2,10)
Now, we have problems. We had 13 as a win by splitting it into 5 and 8, but these are now both decision points. We can find a definite lose by splitting 13 into 6 and 7, but is 13 a lose or a decision point. That is, is 5 and 8 still a winning split ?
Why can't we choose 11 and 2 ? Well, the 14 example showed that if you leave one decision point, you will lose. So, having 2 decision points is the only strategy we have left.
If being left with only one decision point means that you will win, the best strategy is now to try and force your opponent to split the other decision point first. Therefore, both players will try to keep two decision points in the game by splitting a decision point pile into two new piles, one of which is another decision point pile. For example 8 into 3 and 5.
So, if 13 is split into 8 and 5, the opponent will split the 8 into 5 and 3 giving us 5,5 and 3. The three is split leaving 5 and 5. Your opponent has to split one of the decision points thus leaving you as the winner. Therefore, 13 into 8 and 5 is a winning move, therefore 13 is itself a decision point. It should be noted that playing 5 and 8 can also guarantee a loss; you simply play the losing move when you split the last decision point.
So, the strategy of keeping two decision points in the game requires us to know how many splits can we make to a decision point pile in order to keep a decision point pile in the game.
5 0 MOVES
8->5,3->5 2 MOVES
11->8,3->8 2 + 2 = 4 MOVES
11->5,6->5,4->5,3->5 4 MOVES
13->11 1+4 = 5 MOVES
Given these rules, we shall complete the table up to 20.
13 ? W (5,8) L (5,8)
14 ? W (4,10) L (2,12)
15 W (6,9)
16 ? W (5,11) L (5,11)
17 ? W (7,10) L (2,15)
18 W (3,15)
19 ? W (8,11) L (8,11)
20 L
Note, how 16 and 19 are wins by splitting into two even decision points, while 18 is not a decision point even though it could be split into 5 and 13. This is because 5 is an even decision point, while 13 is an odd decision point.
Note, that we haven't yet analysed the misere version of the game.EVALUATION FUNCTIONS
The aim of evaluation functions is to give the best guide possible of the worth of a position in terms of the likelihood that the program can win from this position relative to that of other similar positions. Each position is one that might occur in the lookahead. The best evaluation functions are based upon the experience of experts or people knowledgeable about the game and include paramters, usually. The parameters can be varied both in value and by selecting particular ones ofr different parts of the game. Examples of evaluation functions which are estimates not accurate calculations are available for a variety of games. In Tictactoe or noughts and crosses or OXO we have
y1 + 5y2 + 25 y3
where a mark is a nought or a cross, and
where y1 is the number of clear lines with one mark
where y2 is the number of clear lines with two marks
where y3 is the number of clear lines with three marks
all lines and there are eight in OXO must be clear or unblocked to score thus a line with both noughts and a cross on it are ignored.
MINIMAXING
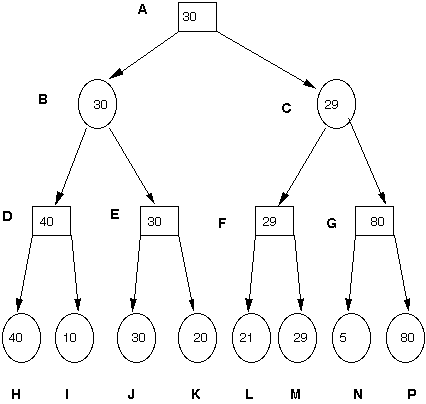
An example of minimaxing using Slagle's notation & illustrating the use of breadth first is given in figure A. The order in which the nodes is created is most important and furthermore the number of nodes held at once is also a critical factor when we use depth first . The nodes have been created in the order indicated by the letters and at any time not all the nodes need to be present, which is a tremendous advantage. The successive stages of creation are indicated in figure B.
ALPHA BETA PRUNING
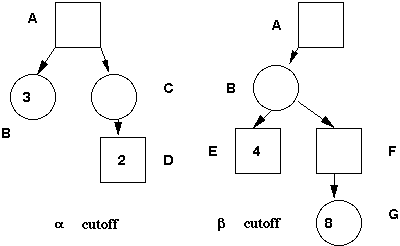
The alpha beta procedure is sometimes called backward pruning and has a modified depth first generation procedure. The purpose of this procedure is to reduce the amount of work in genrating useless nodes, or nodes that will not effect the outcome, and is based upon common sense or basi logic. In the diagrams below, in figure C, once node D is evaluated at 2 we have an alpha cutoff as node A must be at least 3 and so C being at most 2 can have no possible effect. Likewise in the other diagram when node G is evaluated at 8 then node B is at most 4 and so further generation of nodes is not needed.